题目内容
（请给出正确答案）
[主观题]
设＜ G,*＞是一个群,而a∈G,如果f是从G到G的映射.使得对于每一个x∈G,都有f（x)=a*x*a-1,试证明:f是一个从G到G上的自同构。
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
更多“设＜ G,*＞是一个群,而a∈G,如果f是从G到G的映射.使…”相关的问题
设(G，△)是一个群，而a∈G．如果f是从G到G的映射，使得对于每一个x∈G，都有f(x)=a△x△a-1，证明：f是从G到G的自同构．
设f1、f2都是从代数系统(A，★)到(B，*)的同态．设g是从A到B的一个映射，使得对任意a∈A都有g(a)=f1(a)*f2(a)．证明：如果(B，*)是一个可交换半群，那么g是由(A，★)到(B，*)的同态．
设f和g都是群(G1，★)到群(G2，*)的同态映射，证明：(C，★)是(G1，★)的一个子群，其中，C={x|x∈G1，且f(x)=g(x)}．
设X，Y，Z均为距离空间，f是X到Y中的映射，g是Y到Z中的映射，证明：
(1)若f，g连续，则复合映射
(2)若f，g是一对一的，则gοf，也是一对一的，反之若gοf是一对一的，则f是一对一的。举例说明，此时g未必是一对一的。试找出gοf是一对一的充分必要条件；
(3)f，g是同胚映射，则gοf也是同胚映射。
设(G，*)是一个独异点，并且对于G中的每一个元素x都有x*x=e，其中e是单位元．证明：(G，*)是一个阿贝尔群．
设G是一个群，a∈G。映射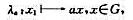
叫做G的一个左平移。证明：
(i)左平移是G到自身的一个双射;
(ii)设a，b∈G，定义λaλb=λa·λb(映射的合成)，则G的全体左平移{λa|a∈G}对于这样定义的乘法作成一个群G';
(iii)G≌G'。
设＜G,*＞是一个群，若在G上定义运算·，使得对于任何元素x,y∈G都有x·y=y*x.证明：＜G,·＞也是群
假设f：A→B并定义一个函数G：B→p(A)，对于b∈B，G(b)={x∈A|f(x)=b}，证明：如果f是A到B的满射，则G是入射的。
证明：如果f是由(A，★)到(B，*)的同态映射，g是由(B，*)到(G，△)的同态映射，那么，
是由(A，★)到(G，△)的同态映射。
