 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
设G与G'都是群,f是群G到G'的同态映射,a∈G.(1)证明若a的阶是有限的,则f(a)的阶也是有
设G与G'都是群,f是群G到G'的同态映射,a∈G.(1)证明若a的阶是有限的,则f(a)的阶也是有
设G与G'都是群,f是群G到G'的同态映射,a∈G.
(1)证明若a的阶是有限的,则f(a)的阶也是有限的,且|f(a)|、整除|a|.
(2)如果f(a)的阶是有限的,那么a的阶一定是有限的吗?证明你的结论.
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“设G与G'都是群,f是群G到G'的同态映射,a∈G.(1)证…”相关的问题
更多“设G与G'都是群,f是群G到G'的同态映射,a∈G.(1)证…”相关的问题
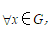 ,证明f是G的自同构.
,证明f是G的自同构.















